Generic coordinate transformations are available using the procedures
Example 2.31 shows how to retrieve the mwcs information from an image. Example 2.32 will create a WCS such that the world system is centered on an image and the axis decrease value with increasing pixel value. Example 2.33 shows some examples of transforming coordinates with an already opened mwcs object. Assume that the mwcs object describes a transformations for a three dimensional image. The final example (Example 2.34) prints all the values for all the attributes of all the axis of an image's mwcs.
This next example creates a WCS such that the world system is centered on an image and the axis decreases with increasing pixel values.
The following examples transform coordinates with an already opened mwcs object. Assume that the object describes a transformation for a 3-dimensional image.
The example below prints all values for all attributes of all axes of an image's mwcs.
Generated with CERN WebMaker
Coordinate Systems
The mwcs package defines three coordinate systems between which two transformations are performed. The three coordinate systems are defined as follows:
The coordinate systems are referred to by the strings physical, logical, and world. Note that there may be many Wterms specified for any one WCS. The world system refers to the current Wterm defined. Other Wterms are referred to by user-supplied names (see mw_newsystem()) and can be made the current system by mw_ssystem(). The two transformations are specified by the Lterm and the Wterm. The Lterm specifies a linear transformation between the physical and logical coordinate systems. The Wterm specifies the transformation between the physical and world coordinate systems The general flow of transforming coordinates is:
A WCS always has a number of predefined attributes, and may also have any number of user defined, or WCS specific, attributes. These are defined when the WCS is created, in the wattr argument input to mw_swtype(), or in a subsequent call to mw_swattrs(). The WCS attributes for a specific axis may be queried with the function mw_gwattrs(). Attribute values may be modified, or new attributes defined, with mw_swattrs(). The issue of WCS attributes is discussed further in the next section. The WCS attributes which can be set by the wattr term consist of a number of standard attributes, plus an arbitrary number of additional WCS specific (application defined) attributes. The following standard attributes are reserved (but not necessarily defined) for each WCS: 
Table 2.76: WCS Standard Attributes.
In addition, the following are defined for the entire WCS, regardless of the axis: 
Table 2.77: WCS Attributes.
For example, to determine the WCS type for axis 1:
call mw_gwattrs (mw, 1, "wtype", wtype, SZ_WTYPE)
Axis Mapping
The coordinate transformation procedures include support for a feature called axis mapping, used to implement dimensional reduction. A example of dimensional reduction occurs in imio, when an image section is used to specify a subraster of an image of dimension less than the full physical image. For example, the section might specify a one dimensional line or column of a two or higher dimensional image, or a two dimensional section of a three dimensional image. When this occurs the application sees a logical image of dimension equal to that of the image section, since logically an image section is an image. Dimensional reduction is implemented in mwcs by a transformation on the input and output coordinate vectors. The internal mwcs coordinate system is unaffected by either dimensional reduction or axis mapping; axis mapping affects only the view of the WCS as seen by the application using the coordinate transformation procedures. For example, if the physical image is an image cube and we access the logical image section [*,5,*], an axis mapping may be set up which maps physical axis one to logical axis one, physical axis two to the constant 5, and physical axis three to logical axis two. The internal system remains three dimensional, but the application sees a two dimensional system. Upon input, the missing axis y=5 is added to the two dimensional input coordinate vectors, producing a three dimensional coordinate vector for internal use. During output, axis two is dropped and replaced by axis three. The axis map is entered with mw_saxmap() and queried with mw_gaxmap(). Here, axno is a vector, with axno[i] specifying the logical axis to be mapped onto physical axis i. If zero is specified, the constant axval[i] is used instead. Axis mapping may be enabled or disabled with a call to mw_seti(). Axis mapping affects all of the coordinate transformation procedures and all of the coordinate system specification procedures. Axis mapping is not used with those procedures which directly access or modify the physical or world systems (e.g., mw_slterm() or mw_swterm()) since full knowledge of the physical system is necessary for such operations. Object Creation and Storage
The mwcs interface routines used to create or access mwcs objects, or save and restore mwcs objects in external storage, are summarized below.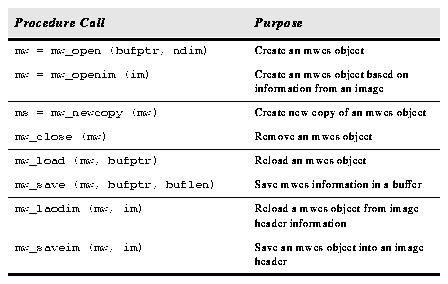
Table 2.78: MWCS Object Functions.
mw_open() creates a new mwcs object and a pointer to it is returned. If bufptr is NULL, then an identity transformation is created with the dimension specified by ndim. If bufptr is pointing to an encoded mwcs buffer, the mwcs object is loaded with that information mw_openim() initializes an mwcs object with data from the image pointed to by the image descriptor im. If the image contains no mwcs information, an identity transformation is loaded instead. mw_newcopy() creates a new mwcs object that is a copy of the mwcs object specified by mw. mw_close() deallocates the memory structures associated with the mwcs object mw. mwcs objects can be saved in an encoded, machine-independent format in a memory array. This array can then be saved into a file, sent over the network, etc. mw_save() will save the contents of the mwcs object mw into the memory pointed to by the char pointer bufptr. If bufptr is NULL, a memory buffer is allocated whose pointer is returned in bufptr. If bufptr is not NULL, the buffer, of length buflen, is used (and resized if necessary). The length of the buffer is returned. The buffer bufptr can be used in the calls mw_open() and mw_load(). mw_load() reloads the mwcs object mw with information contained in the buffer bufptr saved by mw_save(). mw_loadim() reloads an existing mwcs object mw with information from the image pointed to by the image descriptor im. mw_saveim() saves the contents of the mwcs object mw into the image pointed to by the image descriptor im. Coordinate Transformation Procedures
The mwcs procedures used to perform coordinate transformations are summarized below.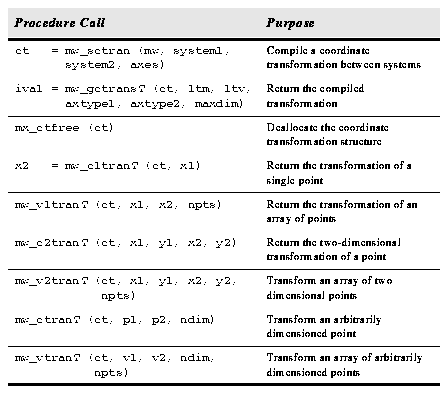
Table 2.79: MWCS Coordinate Transformation Procedures.
The mw_sctran() procedure precomputes the transformation from one coordinate system, system1, to another, system2, for the specified axes in the mwcs object mw returning a pointer to the optimized coordinate transformation. This pointer, ct is used in the subsequent coordinate transformation calls, mw_c2tran(), etc. The axes argument is a bitfield that represents which axes the transformation should apply to. That is, if you wish to transform the first two axes (x and y), set axis = 3. The mw_gctrant() procedure retrieves a compiled linear transformation and returns the dimensionality of the transformation. The argument ltm contains the coefficient determination matrix, ltv contains the translation vector, axtype1 contains the axis types for each of the axes in the source coordinate system, axtype2 contains the axis types in the destination coordinate system, and maxdim specifies the maximum dimensionality that the arrays can handle. Coordinate System Specification
The procedures used to enter, modify, or inspect the mwcs logical and world coordinate transformations are summarized below. 
Table 2.80: MWCS System Specification Functions.
The procedures mw_sltermT() and mw_gltermT() are used to directly enter or inspect the Lterm of the mwcs object mw, which consists of the linear transformation matrix ltm and the translation vector ltv, both of dimension ndim, defining the transformation from the physical system to the logical system. 
Table 2.81: Axis Specification Functions.
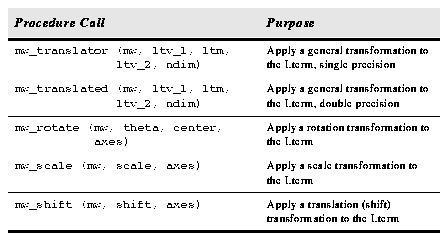
Table 2.82: Applying Transformations to Lterm.
If the logical system undergoes successive linear transformations, mw_translate() may be used to translate, rather than replace, the Lterm of the mwcs object mw, where the given transformation matrix and translation vector refer to the relative transformation undergone by the logical system. This will always work since the Lterm is initialized to the identity matrix when a new mwcs object is created. See also mw_rotate(), mw_scale(), and mw_shift(). mw_translate(), mw_rotate(), mw_scale, and mw_shift. The mw_translate() procedure is the most general, with the others provided as convenient front-ends. Note that mw_rotate() rotates the Lterm of the mwcs object mw through the angle theta, specified in radians, about an arbitrary point center for the specified axes. The axes argument is a bitfield representing which axes to which the transformation applies. That is, each bit represents an axis to transform. mwcs Parameters
The mwcs status procedures, used to query or set the mwcs parameters, are as follows.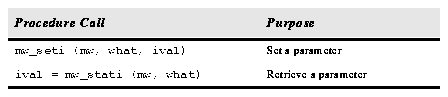
Table 2.83: MWCS Status Procedures.
Table 2.84: MWCS Interface Parameters.
MW_NDIM may differ from MW_NPHYSDIM if dimensional reduction has been specified and axis mapping is enabled. MW_NWCS returns the number of WCS currently defined; at least two WCS are always defined, i.e., the logical and physical systems (the world system will default to the physical system if not otherwise defined). Matrix Routines
The following general purpose matrix manipulation routines are used internally within the interface to compile or evaluate transformations, and may be useful in applications code as well.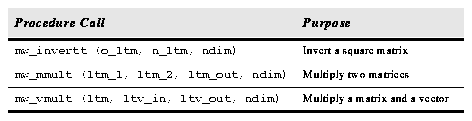
Table 2.85: Matrix Routines.
Each is implemented for both real and double variables. They operate on square matrices whose dimensions are specified by ndim, i.e., ltm[ndim,ndim]. Examples
This section presents of a few simple examples to demonstrate the basic workings of the mwcs interface. The examples will be code fragments showing the necessary declarations, etc., and are not intended to be complete programs. 
